Liebe Leser,
ich freue mich sehr, den dritten sehr interessanten Beitrag der Artikelserie „Sportwetten als (Risiko-)Investment“ von Phil, dem Betreiber von betiando.com, veröffentlichen zu dürfen. Wie berechnet man Wettquoten:
Nachdem ich in meinem letzten Blogbeitrag das Value-Prinzip bei Sportwetten erklärt habe, möchte ich nun darauf eingehen, wie man eigentlich ein Modell zum Quoten Berechnen erstellen kann. Sobald man dazu in der Lage ist, eigene Fussball-Quoten anzugeben, kann man diese mit den Wettquoten am Wettmarkt abgleichen und entsprechende Wetten platzieren. Langfristigen Gewinn erreichen Sie dann, wenn Ihre eigenen Fussball Quoten die Realität besser beschreiben als der Wettmarkt.
Ich möchte die Herleitung von Wettquoten anhand von Fußball erklären. Prinzipiell kann die Methodik zum Herleiten von Wettquoten auch auf andere Sportarten übertragen werden, jedoch ist Fußball in Deutschland sehr stark verbreitet und beinahe jeder ist mit den Regeln vertraut. Bei Fußballspielen kann man auf verschiedenen Wettmärkten aktiv sein, wie z.B. 1×2-Markt, over/under 2,5 oder Endergebnis. Ich möchte hier ein Modell herleiten, welches die Wahrscheinlichkeiten für Endergebnisse liefert. Mit Hilfe dieser Wahrscheinlichkeiten können dann natürlich auch die Wahrscheinlichkeiten für den 1×2 oder over/under 2,5 Markt hergeleitet werden.
📣 Passives Einkommen: Endlich Anleitungen, die funktionieren!
Passives Einkommen zu generieren ist möglich ㅡ Mit diesem Buch!
💡 Hier mein Review zum Buch lesen.
—
Bei Links in diesem Angebot handelt es sich um sog. Affiliate-/Werbelinks. Für jeden Kauf oder jede Anmeldung über einen Affiliate-Link erhält der Webseitenbetreiber eine Provision. Für den Nutzer entstehen dabei KEINE zusätzlichen Kosten.
Diese Webseite finanziert sich hauptsächlich über sog. Affiliate-Links = * (Werbung). Für jeden Kauf oder jede Anmeldung über einen Affiliate-Link erhält der Webseitenbetreiber eine Provision. Für den Nutzer entstehen dabei KEINE zusätzlichen Kosten. Weitere Informationen
Mein Anspruch: Ich empfehle und bewerte nur Produkte, Anbieter oder Dienstleistungen, die ich inhaltlich und fachlich beurteilen und empfehlen kann. Eingeschränkte oder individuelle Empfehlungen werden dabei zusätzlich erläutert.
Vielen Dank für Deine Unterstützung! 💙
Ein klassisches Modell zur Vorhersage von Fußballspielen
Das Modell, das wir im Folgenden gemeinsam erarbeiten wollen, ist an diese Publikation von Maher aus dem Jahr 1982 angelehnt. Im Laufe der Zeit wurde dieses Modell immer weiter verfeinert, um die Realität besser zu beschreiben, doch der Grundgedanke entspricht auch noch heute der Herangehensweise der Wettindustrie. Buchmacher beschäftigen Mathematiker und Statistiker um solche Modell zu entwickeln und Fussball Quoten berechnen zu können. Wenn Sie langfristig mit Sportwetten erfolgreich arbeiten möchten, müssen Sie bessere Modelle entwickeln oder die Schwachstellen bestehender Modelle ausnutzen.
Dieser Beitrag wird etwas Mathematik-lastig sein. Ich möchte jedoch die Zusammenhänge möglichst greifbar und anhand von Beispielen erklären. Daher nehmen wir nun an, dass ein Fußballspiel bevorsteht, wie z.B. das WM Finale 2014 zwischen Deutschland und Argentinien. Sie werden dann für sich entscheiden, welches Endergebnis Sie für am wahrscheinlichsten halten. Beispielsweise können Sie einen leichten Vorteil für Deutschland erkennen und erwarten ein 2:1. Ein Freund von Ihnen sieht z.B. einen größeren Vorteil für Deutschland und hält ein 3:1 für am wahrscheinlichsten.
Sie und Ihr Freund haben soeben eine Anzahl an Toren für Deutschland und Argentinien definiert, die Sie für am wahrscheinlichsten halten. Alternativ zu dieser Größe können Sie auch einen Torerwartungswert definieren. Dieser Wert gibt an, welche Anzahl an Toren im Mittel zu erwarten ist. Um den Erwartungswert zu erklären, möchte ich auf das Würfel-Experiment zurückkehren. Beim idealen Würfel ist das Auftreten aller Zahlen von 1-6 gleich wahrscheinlich, die Wahrscheinlichkeit ist jeweils 1/6. Wenn Sie diese Wahrscheinlichkeiten mit den möglichen Ausgängen, den Zahlen 1-6 multiplizieren und aufsummieren, also 1/6 * 1 + 1/6 * 2 + 1/6 * 3 + 1/6 * 4 + 1/6 * 5 + 1/6 *6 erhalten Sie einen Erwartungswert von 3,5. Wenn Sie sehr oft würfeln und die Summe aus der Augenzahl bilden, diesen Wert durch die Anzahl an Würfe teilen, werden Sie auf einen Wert nahe bei 3,5 kommen. Genauso können Sie dieses Konzept auf ein Fußballspiel übertragen. Wenn das WM Finale zwischen Deutschland und Argentinien z.B. 10 mal unter den gleichen Umständen wiederholbar wäre, dann bilden Sie den Mittelwert der Tore je Mannschaft. Dieser Mittelwert entspricht dem Erwartungswert. Der Erwartungswert kann bei unserem Fußballbeispiel nicht hergeleitet werden, sondern muss abgeschätzt werden.
Die Frage ist nun, wie man mit Hilfe dieses Erwartungswertes die Wahrscheinlichkeiten für alle möglichen End-Ergebnisse ableiten kann. Wenn Sie z.B. von Deutschland 2 Tore erwarten, werden Sie auch eine gewisse Wahrscheinlichkeit für den Fall vorbehalten, dass Deutschland nur 1 Tor oder sogar gar kein Tor schießt. Was Sie also benötigen ist eine Funktion, die 2 Parametern abhängt: Ein Parameter für Ihren Tor-Erwartungswert und ein zweiter Parameter für alle denkbaren Ausgänge (Deutschland schießt 0 Tore, 1 Tor, 2 Tore, 3 Tore, etc).
Die Poisson-Verteilung bei Sportwetten
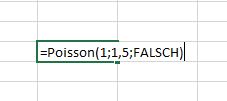
Die Poisson-Verteilung ist genau solch eine Funktion. Sie können z.B. ein Tabellenkalkulationsprogramm wie Excel verwenden und dort die Formel „=Poisson(x; Mittelwert; Kumuliert)“ verwenden. X bezeichnet hierbei alle möglichen Ausgänge, d.h. Deutschland schießt 0 Tore, 1 Tor, 2 Tore, 3 Tore, 4 Tore, usw. Der Mittelwert ist Ihr Tor-Erwartungswert. Die Variable Kumuliert können Sie hier einfach auf Falsch setzen. Wenn Sie z.B. von Deutschland 1,5 Tore erwarten und die Wahrscheinlichkeit berechnen wollen, dass Deutschland 1 Tor schießt bei einer Erwartungshaltung von 1,5 Toren, dann geben Sie folgendes in Excel ein: „=POISSON(1;1,5;FALSCH)“. Excel gibt Ihnen dann einen Wert von ca. 0,33 zurück, was 33% entspricht. Entsprechend können Sie mit „=POISSON(2;1,5;FALSCH)“ auch die Wahrscheinlichkeit berechnen für den Fall, dass Deutschland 2 Tore schießt bei einem Erwartungswert von 1,5. Als Ergebnis erhalten Sie in diesem Fall 25%. Sie können mit dieser Formel die Wahrscheinlichkeit für alle denkbaren Szenarien wie Deutschland 0 Tore, 1 Tor, 2 Tore, usw. berechnen. Natürlich muss die Summe dieser Wahrscheinlichkeiten 100% ergeben, wie Sie leicht selbst überprüfen können.
Im Rahmen dieses Artikels kann ich nicht darauf eingehen, weshalb die Poisson Verteilung Sportwetten zum Vorhersagen von Endergebnissen geeignet ist. Das würde den Rahmen dieses Beitrages sprengen. Denkbar sind natürlich auch andere Wahrscheinlichkeitsverteilungen, ich möchte jedoch die Poisson-Verteilung als gegeben annehmen.
Wahrscheinlichkeiten für das Endergebnis
Wir sind nun dazu in der Lage, eine Wahrscheinlichkeit für die Anzahl an Toren einer Mannschaft anzugeben, abhängig vom Torerwartungswert. Wenn wir z.B. von Deutschland 1,5 Tore erwarten, können wir die Wahrscheinlichkeit für 0 Tore, 1 Tor, 2 Tore, usw. angeben. Die Frage ist nun wie man daraus die Wahrscheinlichkeit für ein Endergebnis ableiten kann.
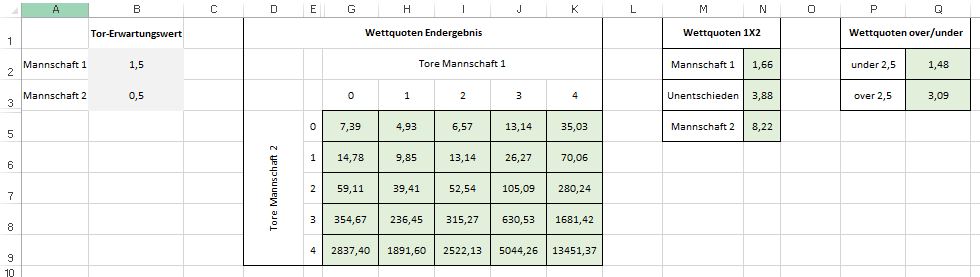
Die Antwort ist relativ einfach: Für die Mannschaft von Argentinien wiederholen wir genau das, was wir für die Anzahl an Toren von Deutschland gemacht haben. Wenn wir z.B. für Argentinien einen Torerwartungswert von 0,5 annehmen, erhalten wir mit Hilfe von „=Poisson(0;0,5;Falsch)“ einen Wert von 61% für den Fall, dass Argentinien 0 Tore schießt. Wir müssen nun lediglich noch die Wahrscheinlichkeiten miteinander multiplizieren: Die Wahrscheinlichkeit, dass Deutschland 1 Tor schießt, bei einem Erwartungswert von 1,5 war 33%. Multiplizieren wir 33% mit 61% erhalten wir eine Wahrscheinlichkeit von 20,3%, dass Deutschland mit 1:0 gegen Argentinien gewinnt. Analog können die Wahrscheinlichkeiten für alle möglichen Endergebnisse berechnet werden.
📣[NEU] Warum eine gewisse Anzahl von Menschen dauerhaft beim Sportwetten gewinnen!?
Schau dir jetzt das Video vollständig an und erfahre, wie du seriös und langfristig mit Sportwetten erfolgreich werden kannst (Auch als Anfänger)
💡 Lese-Tipp auf meinem Blog: Professionelle Sportwetten Strategie entwickeln (Artikelserie).
—
Bei Links in diesem Angebot handelt es sich um sog. Affiliate-/Werbelinks. Für jeden Kauf oder jede Anmeldung über einen Affiliate-Link erhält der Webseitenbetreiber eine Provision. Für den Nutzer entstehen dabei KEINE zusätzlichen Kosten.
Ich würde Ihnen empfehlen, Excel zu starten und ein Spreadsheet aufzusetzen, bei dem man als Benutzer 2 Werte, nämlich die Torerwartungswerte beider Mannschaften, eingeben kann. Das Spreadsheet sollte dann die Wahrscheinlichkeiten für Endergebnisse berechnen. Durch aufsummieren der Wahrscheinlichkeiten kann man dann auch die Wahrscheinlichkeiten für Sieg Mannschaft A, Sieg Mannschaft B und Unentschieden erhalten. Entsprechendes gilt für over/under 2,5 Tore. Falls Sie unsicher sind, können Sie auf meiner Seite nachschauen. Die Wettquote in Dezimalform erhalten Sie einfach, indem Sie den Kehrwert der Wahrscheinlichkeit berechnen, i.e. =1/(…).
Der Erwartungswert für die Anzahl an Toren
Wir haben zwar nun ein mathematisches Modell zur Berechnung der Fussball-Quoten von Endergebnissen – es ist jedoch nicht klar, welche Werte wir für die Tor-Erwartungswerte ansetzen sollen. Hier kommt nun Ihre Kreativität ins Spiel. Im obigen Beispiel haben wir Werte einfach aus dem Bauch heraus angenommen. Sie können jedoch eigene Regeln zur Berechnung des Torerwartungswertes aufstellen, wie z.B. einfach die durchschnittliche Anzahl an geschossenen Toren aus den letzten 3 Spielen. Oder besser der letzten 10 Spiele? Denkbar wäre es auch, einen Heimvorteil einzubeziehen.
In meinem nächsten Blogartikel möchte ich darauf eingehen, wie diese Methode in python umgesetzt werden kann. Ich möchte dann auch verschiedene Varianten für die Berechnung des Tor-Erwartungswertes vorschlagen und die Qualität des Modells anhand der Fussball Quoten und Spielergebnissen der aktuellen Bundesliga-Saison 2014/15 beurteilen.
Bitte beachten: Das ist keine Anlageempfehlung. Sportwetten sind ein Hoch-Risiko-Investment. Wette nicht mit Geld, auf welches Du im Verlustfall nicht verzichten kannst.
Wenn Ihr Fragen, Anregungen oder Kritik loswerden wollt, dann lasst doch ein Kommentar da.
weitere Beiträge der Artikelserie:
#01 – Sportwetten als Investment-Alternative?
#02 – Was ist die Value-Strategie bei Sportwetten?
#04 – Wettstrategien entwicklen, testen und optimieren
💡 Tipp: Wie man systematisch Geld gewinnen kann
Du kannst dich dort auch persönlich mit mir austauschen. Folge jetzt dem exklusiven Telegram-Kanal:
- Der Blog ist tot, es lebe der Blog! - 3. Oktober 2022
- Mein Statement: BaFin Ermittlung bei Cake DeFi [Video] - 10. Januar 2022
- Geld verdienen mit Immobilien (Gastbeitrag) - 30. Oktober 2020



![Schnell Geld verdienen: 15 seriöse & erprobte Möglichkeiten [Update 2023] Schnell Geld verdienen verschiedene Möglichkeiten](https://www.netzjob.eu/wp-content/uploads/2017/11/schnell-geld-verdienen-1.jpg)
![Meine ehrlichen Cake DeFi Erfahrungen [2024] Cashflows auf Kryptos? Screenshot mit der Bezeichnung Cake DeFi Erfahrungen](https://www.netzjob.eu/wp-content/uploads/2021/07/cake-defi-erfahrungen-175x160.jpg)
![Meine ehrlichen ProfitWallet Erfahrungen [Einschätzung & Anleitung] Meine ProfitWallet Erfahrungen als Grafik aus Logo und Schriftzug](https://www.netzjob.eu/wp-content/uploads/2022/08/profitwallet-erfahrungen-netzjob-175x125.jpg)
Hey,
du wirst aber nicht nur die Poisson-verteilung anwenden, um Value zu berechnen?
lg
Hi,
grundsätzlich können verschiedene Wahrscheinlichkeitsverteilungen verwendet werden um ein Modell zu entwicklen. Das hängt auch sehr stark von der jeweiligen Sportart ab. Gebräuchlich im Bereich Sportwetten-Modellierung sind insbesondere auch die Normalverteilung oder die negative Binomialverteilung. Ein erster Ansatz wäre zu schauen, wie die Ergebnisse verteilt sind, z.B. wieviele Tore schießt die Heimmanschaft/Auswärtsmannschaft, wieviele Punkte erzielt das Heimteam/Auswärtsteam und dann zu prüfen, welche Wahrscheinlichkeitsverteilung die konkrete Verteilung der Ergebnisse am besten verteilt.
Die Wahrscheinlichkeitsverteilung wird lediglich dafür verwendet, um Wahrscheinlichkeiten von möglichen Spielausgängen oder Sportwettbewerben zu berechnen. Ob das Modell value ist muss erst noch verifiziert werden (z.B. durch Backtesting).
Hallo Johannes,
erst mal, super dein Blog, danke für deine Mühe!
Ich habe eine andere Frage:
In einer Fußball-Wettgemeinschaft wird in der Endrunde eines Turniers nur auf Sieg getippt, d.h. man bekommt einen Punkt pro richtig getippten Gewinner. Wenn ich nun 7 Punkte Vorsprung habe und es stehen noch 8 Spiele aus, benötige ich nur noch einen richtigen Tipp, um am Ende zumindest punktgleich mit meinen Verfolgern zu sein (vorausgesetzt, die tippen alles richtig).
1) Wie hoch ist die Wahrscheinlichkeit, bei diesen acht verbleibenden 50:50-Wetten wenigstens einen richtig zu tippen? Oder anders ausgedrückt: wie hoch ist die Wahrscheinlichkeit, es nicht zu schaffen? Und wie errechne ich das?
2) Wie hoch ist die Wahrscheinlichkeit, noch eingeholt bzw. besiegt zu werden?
Ich frage, weil ich das Kunststück fertiggebracht habe, alle verbleibenden Spiele falsch zu tippen, während einer meiner Verfolger es geschafft hat, alle dieser verbleibenden Spiele richtig zu tippen, und das kommt mir ein bisschen vor wie ein negativer Sechser im Lotto, und mich würde die statistische Seite dieses Kunststücks interessieren.
Für deine Hilfe wäre ich dir sehr dankbar!
Tom
Hallo Tom,
vielen Dank für Deine Frage. Du kannst die Wahrscheinlichkeit für Dein Beispiel mit der Binomialverteilung berechnen:
P(X)=(n über k)⋅p^k⋅(1−p)^(n−k)
n: Anzahl der Versuche = 8
k: Anzahl der erfolgreichen Versuche = (Beispiel (1): 1; Beispiel (2): 8)
p: Erfolgswahrscheinlichkeit bei einem Versuch = 0,5
Das (n über k) berechnest Du mit dem Binomialkoeffizient
Beispiel (1):
(n über k) = (8 über 1) = 8
p^k⋅(1−p)^(n−k) = 0,5^1⋅(1-0,5)^(8-1) = 1/256
8⋅(1/256) = 1/32 = 3,125%
Beispiel (2):
(n über k) = (8 über 8) = 1
p^k⋅(1−p)^(n−k) = 0,5^8⋅(1-0,5)^(8-8) = 1/256
1⋅(1/256) = 1/256 = 0,39%
Das gilt natürlich nur für den theoretischen (!) Fall, dass es wirklich eine 50/50 Chance bei „unnatürlichen“ Ereignissen (z.B. Münzwurf) gibt. Wenn es jeweils einen Favoriten bzw. einen Außenseiter gibt, dann gibt es andere Erfolgswahrscheinlichkeiten.
Du hattest eine fast 10x höhere Wahrscheinlichkeit, dass Du gewinnst. Aber, dass nennt man dann wohl Glück bzw. Pech, damit ja jeder Zocker/Spieler zu kämpfen, selbst wenn er einen mathematischen Vorteil besitzt. Je länger man spielt, desto weniger Einfluss hat das „Glück“.
UPDATE:
Mit ist aufgefallen, dass sich hier ein kleiner Denkfehler eingeschlichen hat. Beim Beispiel 1 ist die Formal schon richtig, aber du brauchst ja nur 1x „richtig tippen“. Die weiteren Tipps sind ja dann irrelevant. Demnach müsste die Wahrscheinlichkeit bei 50/50 liegen, wenn ich jetzt nicht schon wieder einen Denkfehler habe.
LG
Hallo Johannes,
Wie du die Quoten für ein exaktes Ergbnis unter Berücksichtigung der Torerwartung beider Teams berechnest ist mir klar. Aber wie berechnest du 1×2 bzw. das über/unter dabei?
Hallo Johannes,
super Artikel von Dir. Nur ist mir nicht klar, wie du nach dem Spreadsheet auf die Werte von 1X2 und over/under kommst, um die mit den Quoten der Buchmacher zu vergleichen, um Value Quoten zu finden.
Danke für dein Feedback
Die Wahrscheinlichkeit für „1“, P(1), erhältst du z. B., indem du die Wahrscheinlichkeiten für alle Heimsiegresultate (1:0, 2:0, 2:1, …) addierst.
Die Quote für Heimsieg Q(1) ist dann: Q(1) = 1 / P(1) .
Analog berechnest du „X“ und „2“.